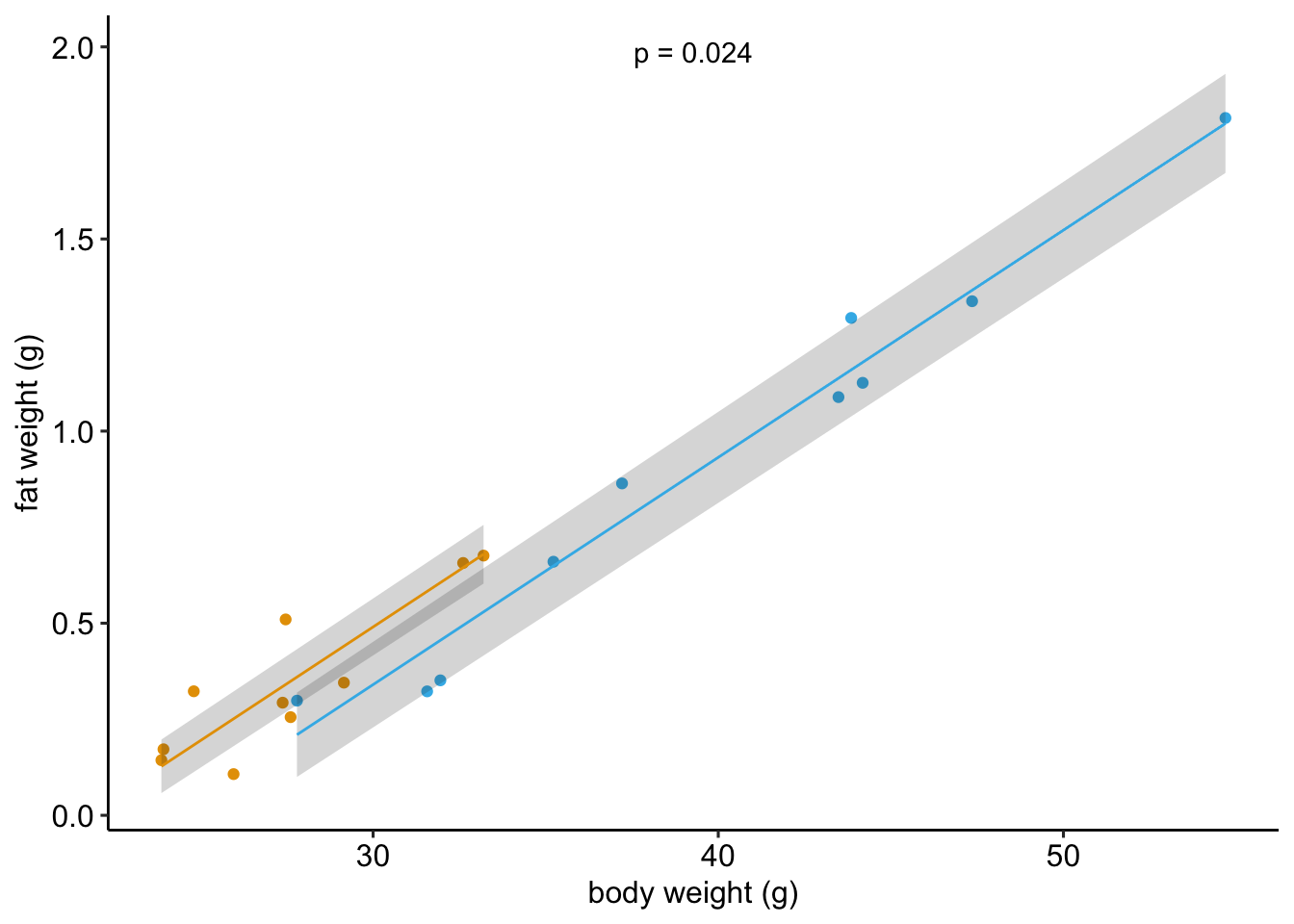
This is fake data that simulates an experiment to measure effect of treatment on fat weight in mice. The treatment is “diet” with two levels: “control” (blue dots) and “treated” (gold dots). Diet has a large effect on total body weight. The simulated data are in the plot above - these look very much like the real data.

The question is, what are problems with using an “ancova” linear model to estimate the direct effect of treatment on fat weight? By ancova linear model I mean

fat ~ body_weight + diet

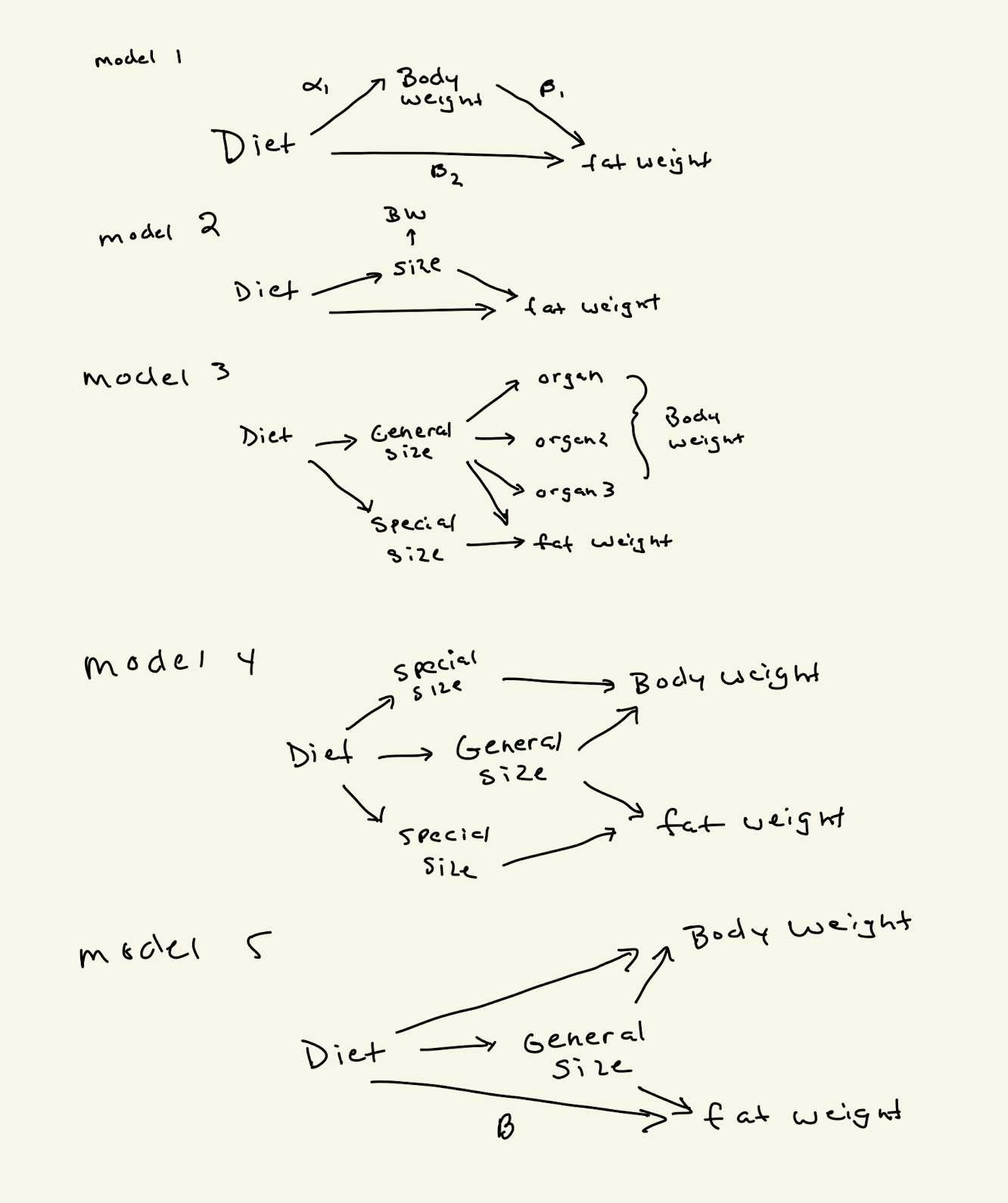
A common assumption of ANCOVA is no treatment effect on the covariate. Here is how I think about the generating model for these data – or a series of generating models – encoded by causal diagrams. The effect we’re trying to estimate is the direct effect of diet on fat (\(\beta_2\) in model 1, or \(\beta\) in model 5). Model 1 is a typical “mediation” model. I don’t care about the mediator, except as a nuissance. Model 2 is a bit more realistic in that body weight is a proxy for “size”. Model 3 is thinking like Sewell Wright in his series of papers on “size factors” - which is the set of foundational papers for causal modeling and DAGs. Model 4 is just collapsing model 3 and model 5 is collapsing it a bit more (the special size factors aren’t measured)

The fake data were generated using model 1 and the ancova linear model estimates the direct effect without bias.

Two issues:

  1. there is an unmeasured variable, U, that has a causal arrow to both body weight and fat weight in model 1.
  2. The covariate is a proxy for the latent factor.

What is the best practice for this problem?