Fake data

Generate \(p\) correlated variables and assign the first to the response (\(\mathbf{y}\)) and the rest to the covariates (\(\mathbf{X}\)). Construct a treatment variable and effect and add this to the response.

n <- 100 # per treatment level - this is modified below
p <- 3 # number of covariates (columns of the data)
pp1 <- p+1
beta_0 <- 0 # intercept

niter <- 2000 # modified below
measure_cols <- c("no_adjust", "imbalance", "all_covariates", "weak_covariates", "strong_covariates")

xcols <- paste0("X", 1:p)
build_ycols <- c("Y_o", xcols)
cor_ycols <- c("Y", xcols)

b_mat <- data.table(NULL)
se_mat <- data.table(NULL)
p_mat <- data.table(NULL)
ci_mat <- data.table(NULL)

for(beta_1 in c(0, 0.2, 0.8)){ # treatment effect on standardized scale
  beta <- c(beta_0, beta_1)
  for(n in c(6, 10, 50)){
    # larger iterations with smaller n
    niter <- round((3*10^4)/sqrt(n), 0)
    niter <- 2000
    
    # repopulate with NA each n
    b <- se <- pval <- ci <- matrix(NA, nrow=niter, ncol=length(measure_cols))
    colnames(b) <- colnames(se) <- colnames(pval) <- colnames(ci) <- measure_cols
    
    Treatment <- rep(c("Cn", "Tr"), each=n)
    X <- model.matrix(formula("~ Treatment"))
    
    for(iter in 1:niter){
      # generate p random, correlated variables. The first is assigned to Y
      fake_data <- fake.X(n*2, pp1, fake.eigenvectors(pp1), fake.eigenvalues(pp1))
      colnames(fake_data) <- build_ycols
      
      # resacale so that var(Y) = 1, where Y is the first column
      fake_data <- fake_data/sd(fake_data[,1])
      
      fake_data <- data.table(fake_data)
      
      # view the scatterplots
      #gg <- ggpairs(X,progress = ggmatrix_progress(clear = FALSE))
      show_it <- FALSE
      if(show_it ==TRUE){
        gg <- ggpairs(fake_data)
        print(gg, progress = F)
      }
      
      # add the treatment effect
      fake_data[, Y:=Y_o + X%*%beta]
      fake_data[, Treatment:=Treatment]
      
      # model 1 - just the treatment
      fit1 <- lm(Y ~ Treatment, data=fake_data)
      res <- coef(summary(fit1))["TreatmentTr", ]
      b[iter, 1] <- res["Estimate"]
      se[iter, 1] <- res["Std. Error"]
      pval[iter, 1] <-res["Pr(>|t|)"]
      ci_i <- confint(fit1)["TreatmentTr",]
      ci[iter, 1] <- ifelse(beta_1 >= ci_i[1] & beta_1 <= ci_i[2], 1, 0)
      res1 <- copy(res)
      
      # model 2 - adjust for imablance
      inc_xcols <- NULL
      for(i in 1:p){
        formula <- paste0(xcols[i], " ~ Treatment")
        fit2a <- lm(formula, data=fake_data)
        if(coef(summary(fit2a))["TreatmentTr", "Pr(>|t|)"] < 0.05){
          inc_xcols <- c(inc_xcols, xcols[i])
        }
      }
      if(length(inc_xcols) > 0){ # if any signifianct effects refit, otherwise use old fit
        formula <- paste0("Y ~ Treatment + ", paste(inc_xcols, collapse=" + "))
        fit2b <- lm(formula, data=fake_data)
        res <- coef(summary(fit2b))["TreatmentTr", ]
        ci_i <- confint(fit2b)["TreatmentTr",]
      }else{
        res <- res1
      }
      b[iter, 2] <- res["Estimate"]
      se[iter, 2] <- res["Std. Error"]
      pval[iter, 2] <-res["Pr(>|t|)"]
      ci[iter, 2] <- ifelse(beta_1 >= ci_i[1] & beta_1 <= ci_i[2], 1, 0)
      
      
      # model 3- adjust for covariates
      (ycor <- abs(cor(fake_data[, .SD, .SDcols=cor_ycols])[2:pp1, 1]))
      mean(ycor)
      
      j <- 2
      for(target_cor in c(0, .2, .4)){
        j <- j+1
        if(target_cor == 0.2){
          inc <- which(ycor < target_cor) # include only weak covariates
        }else{
          inc <- which(ycor > target_cor) # include all OR strong covariates
        }
        if(length(inc) > 0){  # if matches refit, otherwise use old fit
          inc_xcols <- xcols[inc]
          formula <- paste0("Y ~ Treatment + ", paste(inc_xcols, collapse=" + "))
          fit3 <- lm(formula, data=fake_data)
          res <- coef(summary(fit3))["TreatmentTr", ]
          ci_i <- confint(fit3)["TreatmentTr",]
        }else{
          res <- res1
        }
        b[iter, j] <- res["Estimate"]
        se[iter, j] <- res["Std. Error"]
        pval[iter, j] <-res["Pr(>|t|)"]
        ci[iter, j] <- ifelse(beta_1 >= ci_i[1] & beta_1 <= ci_i[2], 1, 0)
      }
    }  
    b_mat <- rbind(b_mat, data.table(n=n, beta_1=beta_1, b))
    se_mat <- rbind(se_mat, data.table(n=n, beta_1=beta_1, se))
    p_mat <- rbind(p_mat, data.table(n=n, beta_1=beta_1, pval))
    ci_mat <- rbind(ci_mat, data.table(n=n, beta_1=beta_1, ci))
  }
}

p_long <- melt(p_mat, measure.vars=measure_cols, variable.name="method", value.name="p")
ci_long <- melt(ci_mat, measure.vars=measure_cols, variable.name="method", value.name="covers")
b_long <- melt(b_mat, measure.vars=measure_cols, variable.name="method", value.name="b")
se_long <- melt(se_mat, measure.vars=measure_cols, variable.name="method", value.name="se")


#ci_long[, .(coverage=sum(covers)/niter), by=.(method, n, beta_1)]

Distribution of estimates

pd <- position_dodge(0.8)
gg <- ggplot(data=b_long, aes(x=factor(n), y=b, fill=method)) +
  geom_boxplot(position=pd) +
  xlab("sample size (per treatment level)") +
  NULL
gg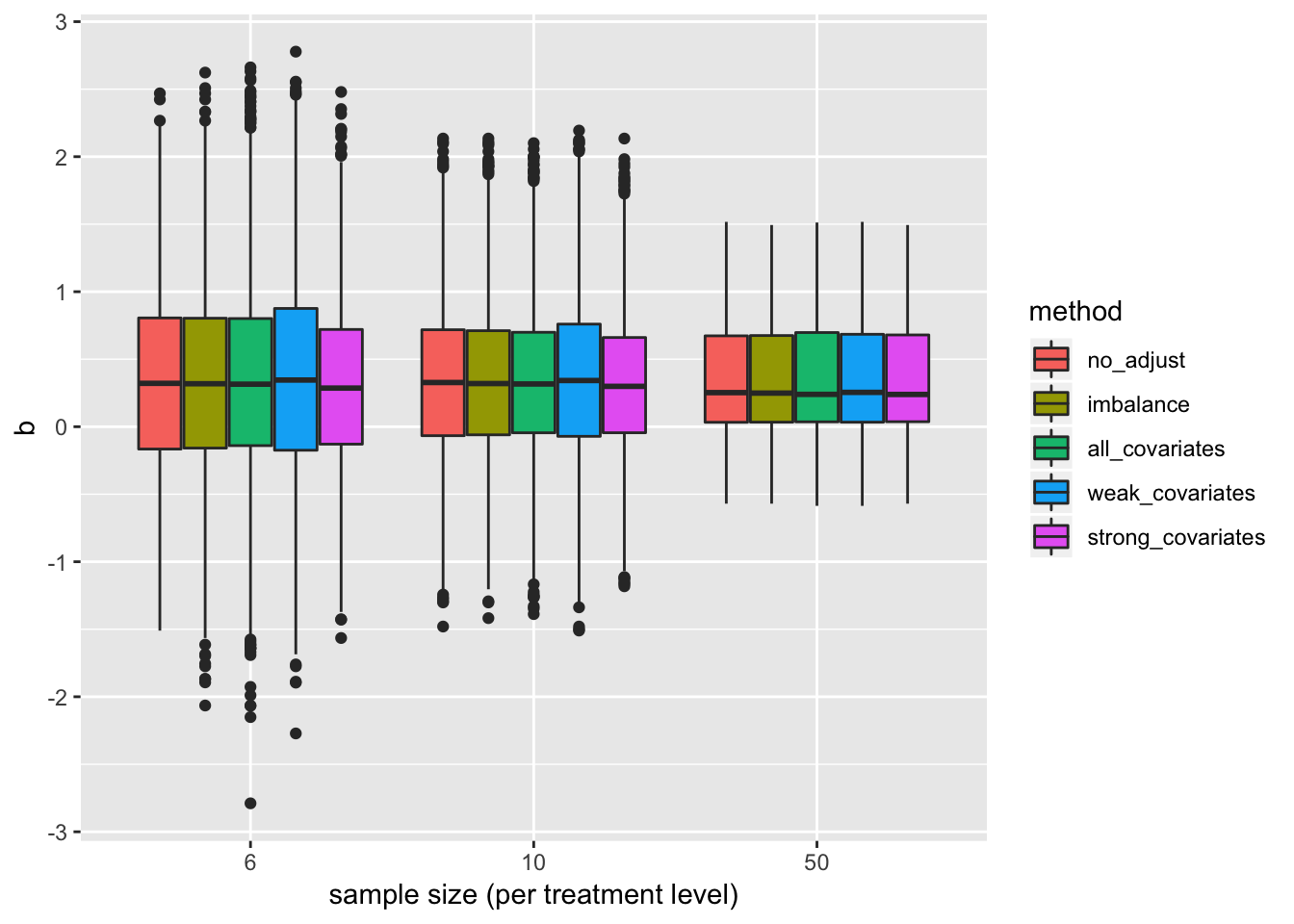

Distribution of SE of estimate

pd <- position_dodge(0.8)
gg <- ggplot(data=se_long, aes(x=factor(n), y=se, fill=method)) +
  geom_boxplot(position=pd) +
  xlab("sample size (per treatment level)") +
  NULL
gg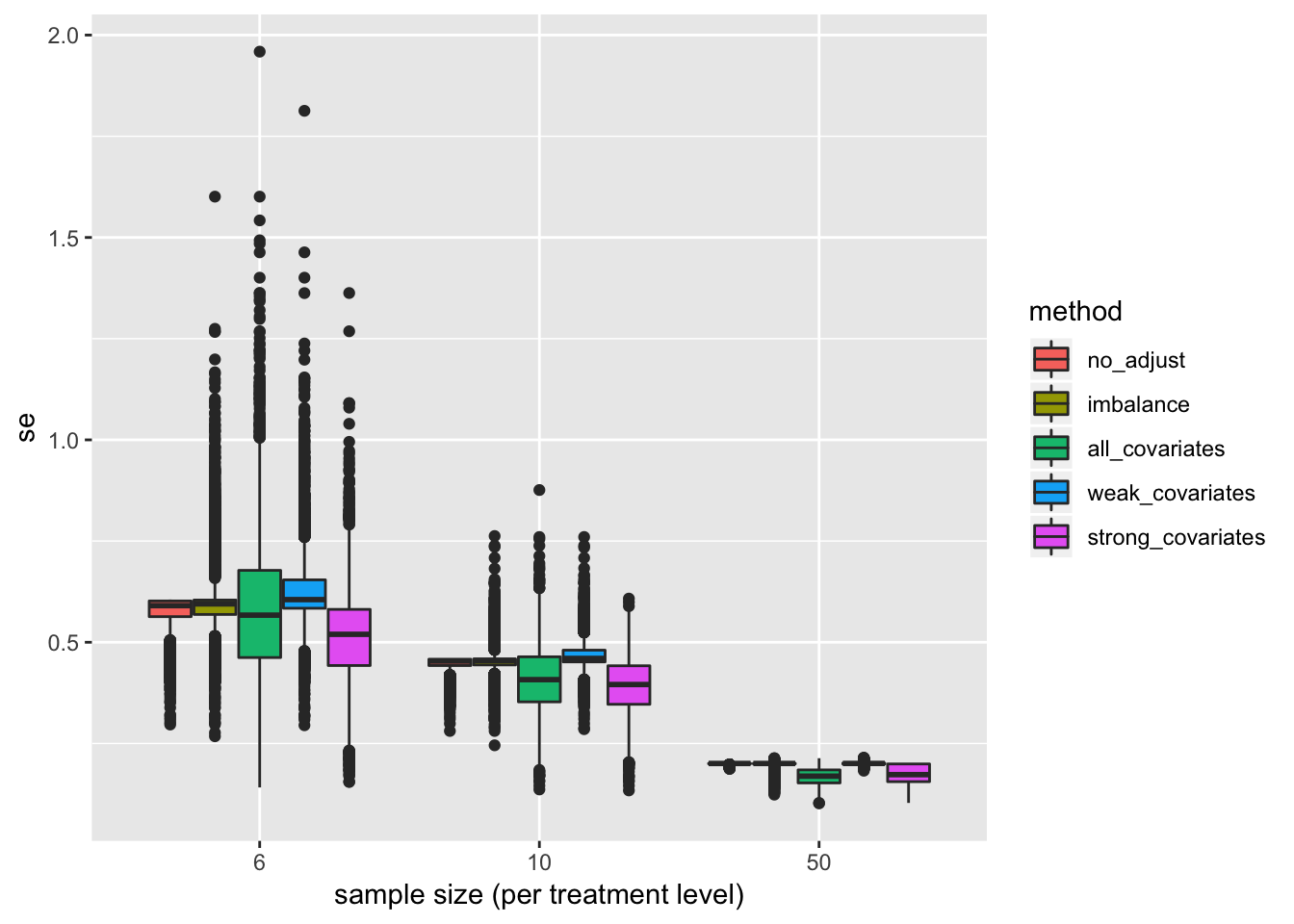

Type I error

# type I
p_sum <- p_long[, .(error=sum(p < 0.05)/niter), by=.(method, n, beta_1)]
pd <- position_dodge(0.8)
gg <- ggplot(data=p_sum[beta_1==0], aes(x=factor(n), y=error, color=method, group=method)) +
  geom_point(position=pd) +
  geom_line(position=pd) + 
  xlab("sample size (per treatment level)") +
  ylab("Type I error") +
  # facet_grid(.~beta_1) +
  NULL
gg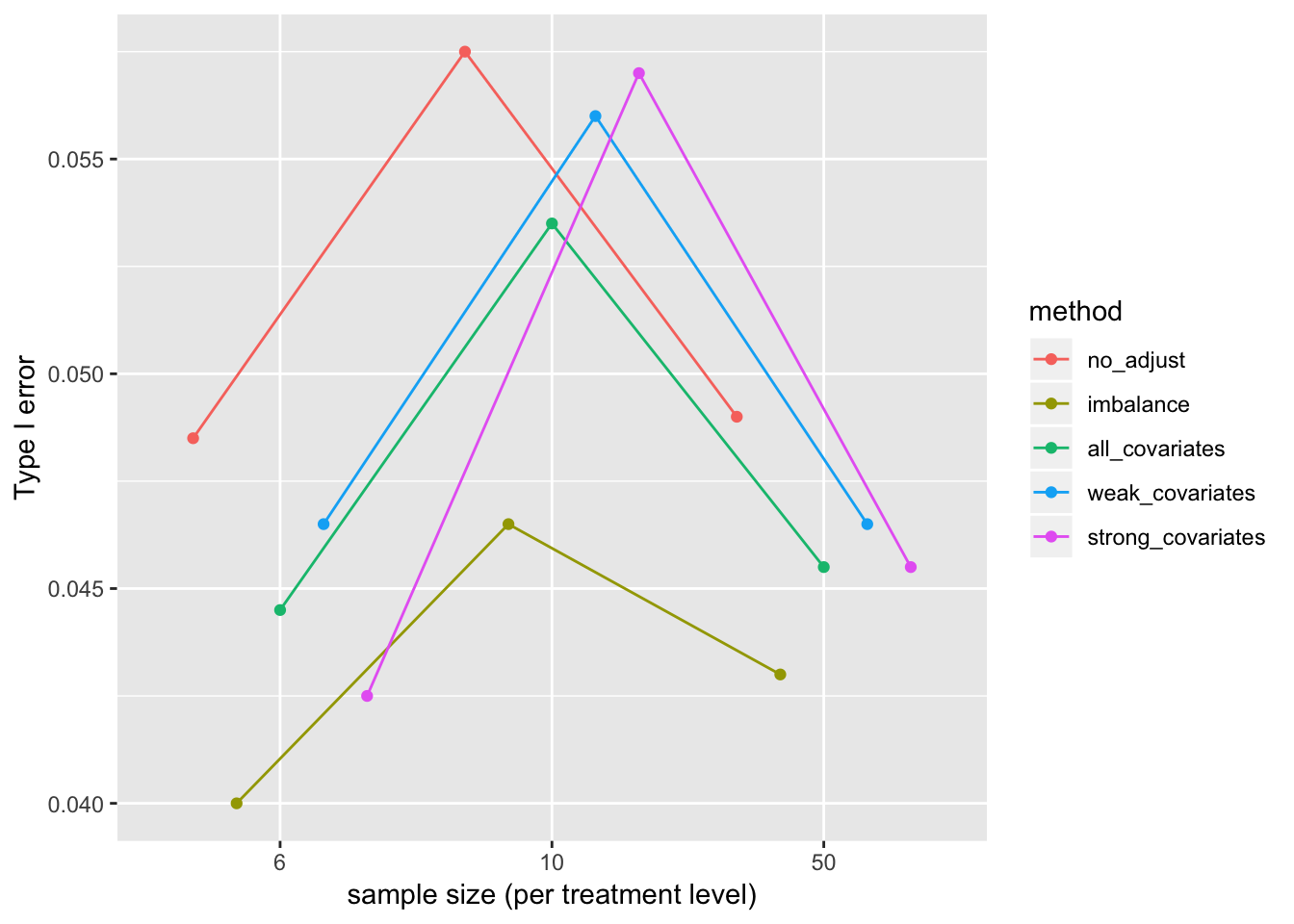

Power

# power
# need p_sum from above
gg <- ggplot(data=p_sum[beta_1!=0], aes(x=factor(n), y=error, color=method)) +
  geom_point(position=pd) +
  xlab("sample size (per treatment level)") +
  ylab("Power") +
  facet_grid(.~beta_1) +
  NULL
gg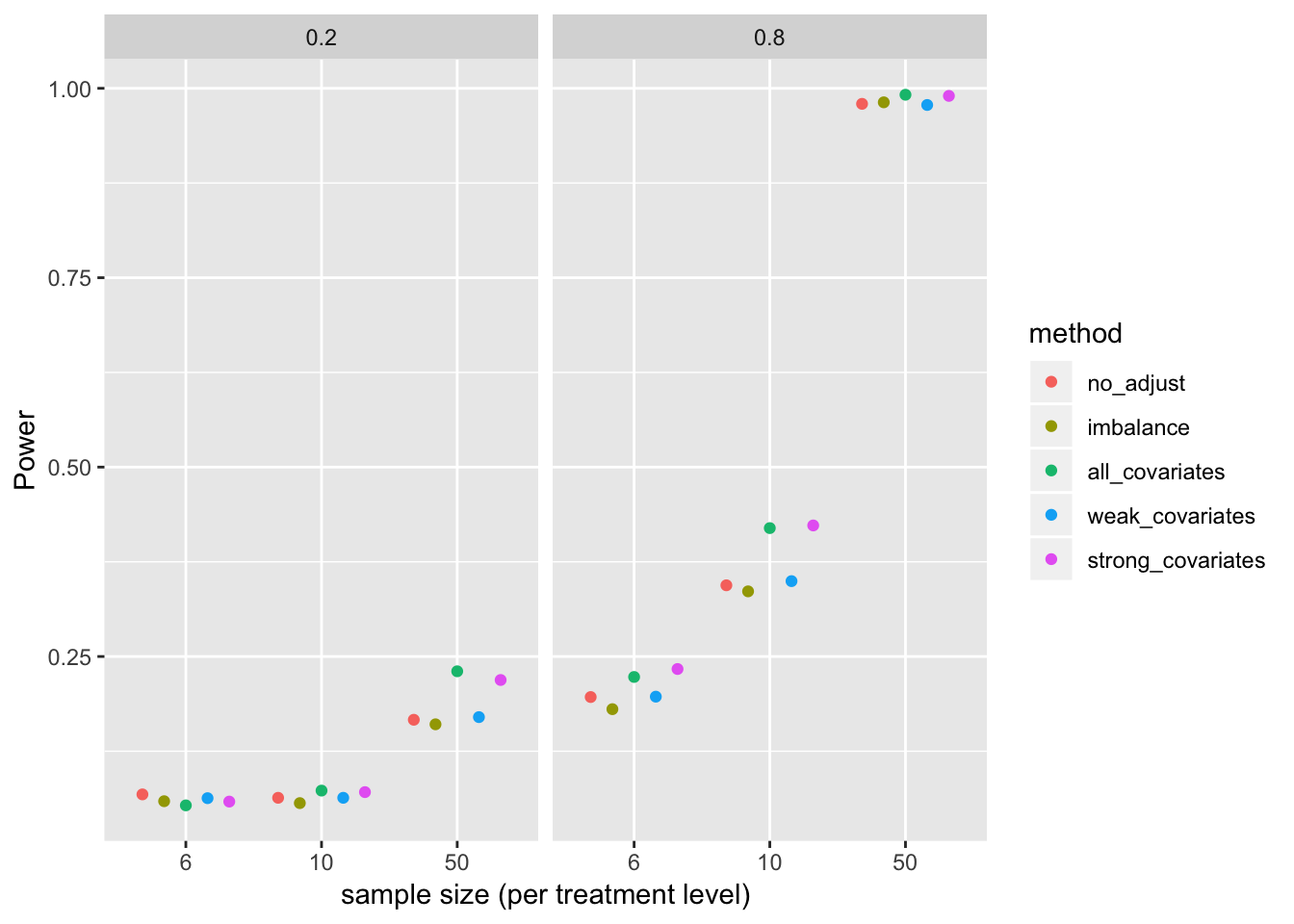

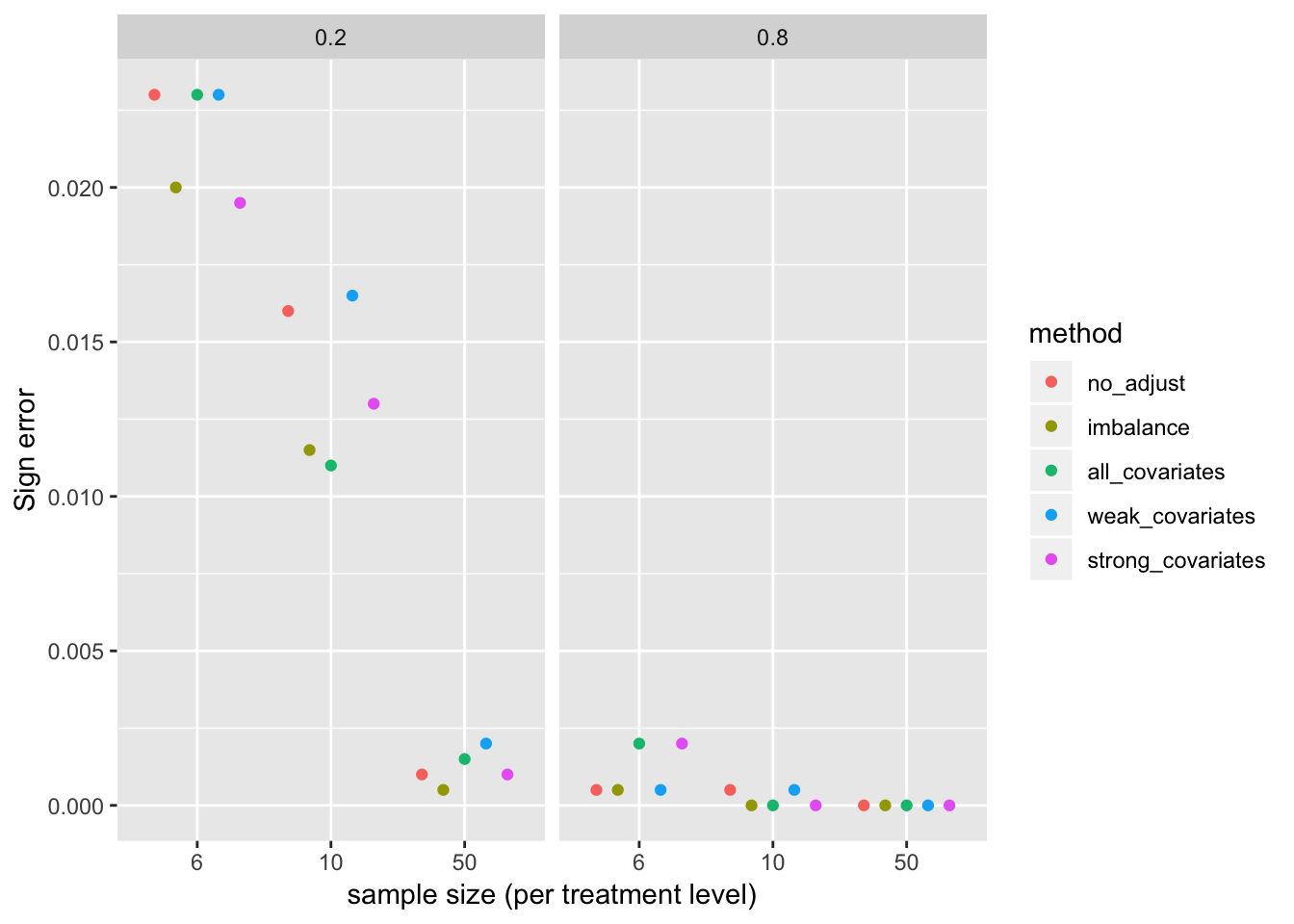
Sign error

# sign error
p_long2 <- cbind(p_long, b=b_long[, b])
sign_error <- p_long2[beta_1 > 0, .(error=sum(p < 0.1 & b < 0)/niter), by=.(method, n, beta_1)]
gg <- ggplot(data=sign_error, aes(x=factor(n), y=error, color=method)) +
  geom_point(position=pd) +
  xlab("sample size (per treatment level)") +
  ylab("Sign error") +
  facet_grid(.~beta_1) +
  NULL
gg