This 1990-wants-you-back doodle explores the effects of a Normality Filter – using a Shapiro-Wilk (SW) test as a decision rule for using either a t-test or some alternative such as a 1) non-parametric Mann-Whitney-Wilcoxon (MWW) test, or 2) a t-test on the log-transformed response. In this strategy, the alternative is used if the Shapiro-Wilk p-value is less than some cut-off (such as 0.05), otherwise the t-test on the untransformed data is used.

TL;DR – Meh. Using a Shapiro-Wilk filter isn’t going to lead to either better or worse inference. That said, if one simply wants a p-value, there are more powerful methods than a t-test on log-transformed data or Mann-Whitney-Wilcoxan..

And of course, none of this addresses estimation itself, just the NHST approach to discovery. This quote from Lumley et al is relevant:

“The major limitation on the t-test and linear regression for inference about associations is not a distributional one, but whether detecting and estimating a difference in the mean of the outcome answers the scientific question at hand.”1

Motivation teaching applied biostatistics to experimental biologists, who learn to do the shapiro-wilks filter from either a previous course, or more likely, its what they commonly read in the literature

Other literature Lumley et al is relevant and Rochon et al

Stuff that needs to be repeatedly stated The failure to reject a null hypothesis does not mean the null hypothesis is true. Or, in the context of this post, we shouldn’t conclude that a sample is “normal” because a Shapiro-Wilk p-value > 0.05. The logic of a test of normality (or homogeneity) before a t-test/ANOVA, then, isn’t consistent with frequentist thinking. But, maybe we should only think of the Normality filter as an objective model check, compared to, say, inspecting a Q-Q plot.

More stuff that needs to be repeatedly stated It is not uncommon to hear and even read that t-tests assume that the response variable is normally distributed. This is not correct. It is the response conditional on the group that is assumed to be normal. Or, equivalently, it is the residuals from a linear model fit to the data that are assumed to be normal. “Conditional on the group” suggests to some textbook authors that normality should be tested on the response variable in each group seperately. The data pass the Normality filter only if the p-value of the SW test is > 0.05 on both tests. This way of thinking about testing the normal assumption is constraining because it doesn’t allow for adjusting for covariates. A better way to think about testing normality is a single test of the residuals of the fit linear model. This way of thinking is better because it naturally leads to model checking of more complex models.

The Normality filter itself raises a few questions that interest me. Given that the p-value of a t-test is not conditional on “passing” the Normality filter…

  1. What is the probability of rejecting the null conditional on only the subset of true nulls that “pass” the Shapiro-Wilk test (that is, how does the filter change the size or Type I error of the t-test)?

  2. What is the probability of rejecting the null conditional on only the subset of false nulls that pass the Shapiro-Wilk test (that is, how does the filter change the power of the t-test)?

Rochon et al. 2 address #1 with a simulation with data generated using normal, uniform, and exponentitial distributions. I don’t know how relevant the uniform and exponential distributions are for most biological data but the exponential at least has some features in common other skewed distributions with a variance that is a function of the mean, including lognormal and gamma (for continuous responses), and a negative binomial (for count data). Rochon’s implementation used R’s “default” exponential settings but the distribution of the performance statistics (type I error and power) will certainly be conditional on the parameterization of the exponential (or gamma or neg binomial) – that is, how much the data are “approximately” normal.

Set up

library(data.table)
library(MASS)
library(ggplot2)
library(ggpubr)
library(cowplot)

do_sims <- FALSE # redo simulations?
fake_data <- function(niter=10^4, n=50, location=0, scale=1, shape=1, effect=0, dist="normal"){

  if(dist=="normal"){
    cn <- matrix(rnorm(n*niter, mean=location, sd=scale), nrow=n, ncol=niter)
    tr <- matrix(rnorm(n*niter, mean=(location + effect), sd=scale), nrow=n, ncol=niter)
    fd <- rbind(cn, tr)
  }
  if(dist=="nb"){ # negative binomial for counts
    cn <- matrix(rnegbin(niter*n, mu=location, theta=shape), nrow=n, ncol=niter)
    tr <- matrix(rnegbin(niter*n, mu=(location + effect), theta=shape), nrow=n, ncol=niter)
    fd <- rbind(cn, tr)
  }
  if(dist=="exp"){ # exponential to reproduce paper
    rate_cn <- 1/location
    rate_tr <- 1/(location + effect)
    cn <- matrix(rexp(niter*n, rate=rate_cn), nrow=n, ncol=niter)
    tr <- matrix(rexp(niter*n, rate=rate_tr), nrow=n, ncol=niter)
    fd <- rbind(cn, tr)
  }
  if(dist=="lnorm"){ # exponential to reproduce paper
    cn <- matrix(rlnorm(niter*n, meanlog=location, sdlog=scale), nrow=n, ncol=niter)
    tr <- matrix(rlnorm(niter*n, meanlog=location, sdlog=scale), nrow=n, ncol=niter)
    fd <- rbind(cn, tr)
  }
  return(fd)
}

filter_stats <- function(fd){
  # outputs SW p for residual, group1, and group2 + unconditional t-test p
  niter <- ncol(fd)
  n <- nrow(fd)/2
  x <- rep(c("a","b"), each=n)
  test_stats_cols <- c("residual", "group1","group2", "p", "p.log", "p.mww")
  test_stats <- matrix(NA, nrow=niter, ncol=length(test_stats_cols))
  colnames(test_stats) <- test_stats_cols

  if(min(fd)==0){
    logfd <- log(fd+1)
    } else{
    logfd <- log(fd) # exponential, gamma
  }
  
  iter <- 1 # for debugging
  for(iter in 1:niter){
    test_stats[iter, "residual"] <- shapiro.test(residuals(lm(fd[, iter] ~ x)))$p.value # using residual
    # test_stats[iter, "group1"] <- shapiro.test(fd[1:n, iter])$p.value # using group variable
    # test_stats[iter, "group2"] <- shapiro.test(fd[(n+1):(2*n), iter])$p.value # using group variable
    test_stats[iter, "p"] <- t.test(fd[, iter] ~ x, var.equal=TRUE)$p.value
    test_stats[iter, "p.log"] <- t.test(logfd[, iter] ~ x, var.equal=TRUE)$p.value
    test_stats[iter, "p.mww"] <- wilcox.test(fd[, iter] ~ x, exact=FALSE)$p.value
  }
  return(test_stats)
}

filter_summary <- function(test_stats, alpha=0.05){
  # note that prob of at least 1 group rejected is
  # 1 - (1-alpha)^2
  niter <- nrow(test_stats)
  
  ###### Shapiro Wilk test stats
  
  # rate of SW rejection using residual
  SW_rej_residual <- sum(test_stats$residual < alpha)/niter
  
  # rate of SW rejection testing each group seperately
  #SW_rej_group <- sum(test_stats$group1 < alpha | test_stats$group2 < alpha)/niter # SW positives using group
  
  ##### t-test stats
  
  # unconditional type I error/power using t-test
  t_unconditional <- sum(test_stats$p < 0.05)/niter
  
  # conditional type I/power of subset that "pass" (not rejected) shapiro wilk test using residuals
  t_pass_residual <- sum(test_stats[residual > alpha, p] < 0.05)/sum(test_stats[,residual > alpha])
  
  # conditional type I/power of subset that "pass" (not rejected) shapiro wilk test using groupwise
  #t_pass_group <- sum(test_stats[group1 > alpha & group2 > alpha, p] < 0.05)/sum(test_stats[, group1 > alpha & group2 > alpha])
  
  # conditional type I/power of subset that "fail" (rejected) shapiro wilk test using residuals
  t_rej_residual <- sum(test_stats[residual < alpha, p] < 0.05)/sum(test_stats[,residual < alpha])
  
  # conditional type I/power of subset that "fail" (rejected) shapiro wilk test using groupwise
  #t_rej_group <- sum(test_stats[group1 < alpha | group2 < alpha, p] < 0.05)/sum(test_stats[, group1 < alpha | group2 < alpha]) # conditional on positive SW on group
  
  
  ##### Mann-Whitney-Wilcoxon test stats
  
  # unconditional type I error/power using MWW
  mww_unconditional <- sum(test_stats$p.mww < 0.05)/niter
  
  # conditional type I/power of subset that "fail" (rejected) shapiro wilk test using residuals
  mww_fail_residual <- sum(test_stats[residual < alpha, p.mww] < 0.05)/sum(test_stats[,residual < alpha])
  
  # conditional type I/power of subset that "fail" (rejected) shapiro wilk test using groupwise
  #mww_fail_group <- sum(test_stats[group1 < alpha & group2 < alpha, p.mww] < 0.05)/sum(test_stats[, group1 < alpha & group2 < alpha])
  
  ##### combined t-test + Mann-Whitney-Wilcoxon test stats

  # conditional type I/power of subset that "pass" (not rejected) shapiro wilk test using residuals
  t_mww_fail_residual <- (sum(test_stats[residual > alpha, p] < 0.05) +
                            sum(test_stats[residual < alpha, p.mww] < 0.05))/niter
  
  # conditional type I/power of subset that "pass" (not rejected) shapiro wilk test using groupwise
  #t_mww_fail_group <- (sum(test_stats[group1 > alpha & group2 > alpha, p] < 0.05) +
  #                     sum(test_stats[group1 < alpha & group2 < alpha, p.mww] < 0.05))/niter

  ##### log-t test stats
  
  logt_unconditional <- sum(test_stats$p.log < 0.05)/niter
  
  # conditional type I/power of subset that "fail" (rejected) shapiro wilk test using residuals
  logt_fail_residual <- sum(test_stats[residual < alpha, p.log] < 0.05)/sum(test_stats[,residual < alpha])
  
  # conditional type I/power of subset that "fail" (rejected) shapiro wilk test using groupwise
  #logt_fail_group <- sum(test_stats[group1 < alpha & group2 < alpha, p.log] < 0.05)/sum(test_stats[, group1 < alpha & group2 < alpha])
  
  ##### combined t-test + log-t test stats

  # conditional type I/power of subset that "pass" (not rejected) shapiro wilk test using residuals
  t_logt_fail_residual <- (sum(test_stats[residual > alpha, p] < 0.05) +
                            sum(test_stats[residual < alpha, p.log] < 0.05))/niter
  
  # conditional type I/power of subset that "pass" (not rejected) shapiro wilk test using groupwise
  #t_logt_fail_group <- (sum(test_stats[group1 > alpha & group2 > alpha, p] < 0.05) +
  #                     sum(test_stats[group1 < alpha & group2 < alpha, p.log] < 0.05))/niter
 

  res <- c(SW_rej.res=SW_rej_residual,
           #SW_rej.group=SW_rej_group,
           t.uncond=t_unconditional,
           t_pass.res=t_pass_residual,
           #t_pass.group=t_pass_group,
           t_rej.residual=t_rej_residual,
           #t_rej_group=t_rej_group,
           
           mww.uncond=mww_unconditional,
           mww_fail.res=mww_fail_residual,
           #mww_fail.group=mww_fail_group,
           t_mww_fail.res=t_mww_fail_residual,
           #t_mww_fail.group=t_mww_fail_group,

           logt.uncond=logt_unconditional,
           logt_fail.res=logt_fail_residual,
           #logt_fail.group=logt_fail_group,
           t_logt_fail.res=t_logt_fail_residual
           #t_logt_fail.group=t_logt_fail_group
           )
  return(res)
}

Normal distribution

No real data are normally distributed so this parameterization of the simulation gives the behavior of the shapiro-wilk filter for data that are effectively normal.

if(do_sims==TRUE){
  set.seed(1)
  base_niter <- 10^4 # target number of shapiro-wilk tests that "pass" (p > 0.05)
  
  mu_i <- 10
  sigma_set <- c(1)
  alpha_set <- c(0.1, 0.05, 0.01)
  n_set <- c(10)
  niter_set <- c(base_niter, base_niter*5, base_niter*10) # more iterations to get more samples that "pass" filter
  res_table <- data.table(NULL)
  gg <- list(NULL)
  list_i <- 0
  for(effect_i in c(0, 0.8)){ # "large" effect
    for(sigma_i in sigma_set){
      list_i <- list_i + 1
      for(i in 1:length(n_set)){
        n_i <- n_set[i]
        niter_i <- niter_set[i]
        fd <- fake_data(niter=niter_i, n=n_i, location=mu_i, scale=sigma_i, effect=effect_i, dist="normal")
        
        res <- data.table(filter_stats(fd))
        for(alpha_i in alpha_set){
          res_table <- rbind(res_table, data.table(
            iter = niter_i,
            mu = mu_i,
            sigma = sigma_i,
            effect = effect_i,
            cn_mean = mean(fd[1:n_i,]),
            cn_sd = sd(fd[1:n_i,]),
            cn_cv = sd(fd[1:n_i,])/mean(fd[1:n_i,]),
            tr_mean = mean(fd[(n_i+1):(n_i*2),]),
            tr_sd = sd(fd[(n_i+1):(n_i*2),]),
            tr_cv = sd(fd[(n_i+1):(n_i*2),])/mean(fd[(n_i+1):(n_i*2),]),
            n = n_i,
            alpha = alpha_i,
            data.table(t(filter_summary(res, alpha=alpha_i)))))
        }
      }
    }
  }
  norm_table <- t(res_table)
  # write to file
  write.table(norm_table, "../output/2019-08-08-norm_table.txt",quote=FALSE, sep="\t")
}else{ # if not true, read file
  norm_table <- read.table("../output/2019-08-08-norm_table.txt", header=TRUE, sep="\t")
}

Type I error

type1 <- norm_table[, 1:3]
colnames(type1) <- c("n=6", "n=10", "n=20")
row.names(type1) <- c(
  "iterations",
  "mu",
  "sigma",
  "effect",
  "Cn mean",
  "Cn sd",
  "Cn cv",
  "Tr mean",
  "Tr sd",
  "Tr cv",
  "n",
  "alpha for normality test",
  "failed normality, rate",
  "t-test: type I, unconditional",
  "t-test: type I, | pass",
  "t-test: type I, | fail",
  "MWW-test: type I, unconditional",
  "MWW-test: type I, | fail",
  "t-MWW: type I",
  "log t-test: type I, unconditional",
  "log t-test: type I, | fail",
  "t-log t: type I"
)
knitr::kable(type1, digits=3, caption="Type I error as a function of n for normal data")
Table 1: Type I error as a function of n for normal data
n=6 n=10 n=20
iterations 10000.000 10000.000 10000.000
mu 10.000 10.000 10.000
sigma 1.000 1.000 1.000
effect 0.000 0.000 0.000
Cn mean 9.998 9.998 9.998
Cn sd 1.004 1.004 1.004
Cn cv 0.100 0.100 0.100
Tr mean 10.001 10.001 10.001
Tr sd 1.001 1.001 1.001
Tr cv 0.100 0.100 0.100
n 10.000 10.000 10.000
alpha for normality test 0.100 0.050 0.010
failed normality, rate 0.097 0.047 0.010
t-test: type I, unconditional 0.048 0.048 0.048
t-test: type I, | pass 0.048 0.049 0.048
t-test: type I, | fail 0.044 0.036 0.021
MWW-test: type I, unconditional 0.040 0.040 0.040
MWW-test: type I, | fail 0.058 0.055 0.073
t-MWW: type I 0.049 0.049 0.048
log t-test: type I, unconditional 0.048 0.048 0.048
log t-test: type I, | fail 0.045 0.038 0.042
t-log t: type I 0.048 0.048 0.048

Summary:

  1. The conditional Type I error of the t-test for the sets that pass the Shapiro-Wilk filter is effectively the nominal value (0.05), as is that for the the unconditional Type I. The conditional Type I error for the sets that fail the filter is small (the test is conservative) but this is irrelevant because these data would be analyzed by Mann-Whitney-Wilcoxon or by a t-test of log-transformed data.
  2. The conditional Type I error for MWW test for sets that fail the Shapiro-Wilk filter is very slightly liberal.
  3. The overal Type I error for the normality-test filter strategy using the Mann-Whitney-Wilcoxon as the alternative is effectively 0.05
  4. The results using the t-test of log transform are very close to nominal regardless of strategy.

These results replicate that in Rochon et al. See also Lumley et al (both are cited above)

Power

type2 <- norm_table[, 4:6] # really power, not type 2
colnames(type2) <- c("n=6", "n=10", "n=20")
row.names(type2) <- c(
  "iterations",
  "mu",
  "sigma",
  "effect",
  "Cn mean",
  "Cn sd",
  "Cn cv",
  "Tr mean",
  "Tr sd",
  "Tr cv",
  "n",
  "alpha for normality test",
  "failed normality, rate",
  "t-test: power, unconditional",
  "t-test: power, | pass",
  "t-test: power, | fail",
  "MWW-test: power, unconditional",
  "MWW-test: power, | fail",
  "t-MWW: power",
  "log t-test: power, unconditional",
  "log t-test: power, | fail",
  "t-log t: power"
)
knitr::kable(type2, digits=3, caption="Power as a function of n for normal data")
Table 2: Power as a function of n for normal data
n=6 n=10 n=20
iterations 10000.000 10000.000 10000.000
mu 10.000 10.000 10.000
sigma 1.000 1.000 1.000
effect 0.800 0.800 0.800
Cn mean 10.000 10.000 10.000
Cn sd 0.997 0.997 0.997
Cn cv 0.100 0.100 0.100
Tr mean 10.799 10.799 10.799
Tr sd 0.999 0.999 0.999
Tr cv 0.093 0.093 0.093
n 10.000 10.000 10.000
alpha for normality test 0.100 0.050 0.010
failed normality, rate 0.104 0.051 0.008
t-test: power, unconditional 0.394 0.394 0.394
t-test: power, | pass 0.396 0.395 0.394
t-test: power, | fail 0.376 0.377 0.412
MWW-test: power, unconditional 0.354 0.354 0.354
MWW-test: power, | fail 0.409 0.433 0.538
t-MWW: power 0.398 0.397 0.395
log t-test: power, unconditional 0.393 0.393 0.393
log t-test: power, | fail 0.377 0.383 0.388
t-log t: power 0.394 0.394 0.394

Summary:

  1. The unconditional Mann-Whitney-Wilcoxon has slightly reduced power relative to the unconditional t-test on either untransformed or log transformed response.
  2. The Mann-Whitney-Wilcoxon for sets that fail has slightly greater power relative to the unconditional t-test on either untransformed or log transformed response.
  3. The combination of 1 and 2 mean that the unconditional t-test, the normality-test filter strategy using Mann-Whitney-Wilcoxon as the alternative, the unconditional t-test on log-transformed responses, and the the normality-test filter strategy using log transformed response as the alternative all have effectively equivalent power.

Right skewed continuous – lognormal

The lognormal distribution is explored with two parameterizations, one with larger skew and one with smaller skew, but still distinct from Normal.

if(do_sims==TRUE){
  set.seed(1)
  base_niter <- 10^4 # target number of shapiro-wilk tests that "pass" (p > 0.05)
  mean_cn <- 10
  sd_cn <- 2
  effect_i <- 2
  
  mu_i <- 0 # exp(x) = 1
  sigma_set <- c(0.8, 0.4)
  alpha_set <- c(0.05)
  n_set <- c(6, 10, 20)
  niter_set <- c(base_niter, base_niter*5, base_niter*10) # more iterations to get more samples that "pass" filter
  res_table <- data.table(NULL)
  gg <- list(NULL)
  list_i <- 0
  for(effect_i in c(0, sd_cn*0.8)){ # "large" effect
    for(sigma_i in sigma_set){
      for(n_i in 1:length(n_set)){
        list_i <- list_i + 1
        niter_i <- niter_set[i]
        fd <- fake_data(niter=niter_i, n=n_i, location=mu_i, scale=sigma_i, effect=0, dist="lnorm")
        
        # set to common CV
        # sd = CV x Mean
        fd <- scale(fd, scale=TRUE)
        sd_cn <- 2
        fd[1:n_i,] <- fd[1:n_i,]*sd_cn + mean_cn # 2 is the sd in the CN
        fd[(n_i+1):(n_i*2),] <- fd[(n_i+1):(n_i*2),]*sd_cn*(mean_cn + effect_i)/mean_cn + mean_cn + effect_i 

        if(n_i == n_set[length(n_set)] & effect_i==0){
          gg_fd <- data.table(x=rep(c("a","b"), each=n_i), fd[, 1:3])
          gg0 <- gghistogram(c(fd))
          gg1 <- ggboxplot(data=gg_fd, x="x", y="V1", add="jitter")
          gg2 <- ggboxplot(data=gg_fd, x="x", y="V2", add="jitter")
          gg3 <- ggboxplot(data=gg_fd, x="x", y="V3", add="jitter")
          gg <- plot_grid(gg0, gg1, gg2, gg3, ncol=4, rel_widths = c(2, 1, 1, 1, 1))
          plot_file_name <- paste0("../images/2019-08-08-gg-s=", sigma_i, ".png")
          save_plot(plot_file_name, gg, base_height = 4, base_width=6)
        }
        
        res <- data.table(filter_stats(fd))
        for(alpha_i in alpha_set){
          res_table <- rbind(res_table, data.table(
            iter = niter_i,
            mu = mu_i,
            sigma = sigma_i,
            effect = effect_i,
            cn_mean = mean(fd[1:n_i,]),
            cn_sd = sd(fd[1:n_i,]),
            cn_cv = sd(fd[1:n_i,])/mean(fd[1:n_i,]),
            tr_mean = mean(fd[(n_i+1):(n_i*2),]),
            tr_sd = sd(fd[(n_i+1):(n_i*2),]),
            tr_cv = sd(fd[(n_i+1):(n_i*2),])/mean(fd[(n_i+1):(n_i*2),]),
            n = n_i,
            alpha = alpha_i,
            #  alpha_2 = 1-(1-alpha_i)^2,
            data.table(t(filter_summary(res, alpha=alpha_i)))))
        }
      }
    }
  }  
  lognorm_table <- t(res_table)
  # write to file
  write.table(lognorm_table, "../output/2019-08-08-lognorm_table.txt",quote=FALSE, sep="\t")
}else{ # if not true, read file
  lognorm_table <- read.table("../output/2019-08-08-lognorm_table.txt", header=TRUE, sep="\t")
}

What the parameterizations look like

knitr::include_graphics("2019-08-08-what-is-the-consequence-of-a-shapiro-wilk-test-of-normality-filter-on-type-i-error-and-power_files/figure-html/2019-08-08-gg-s=0.8.png")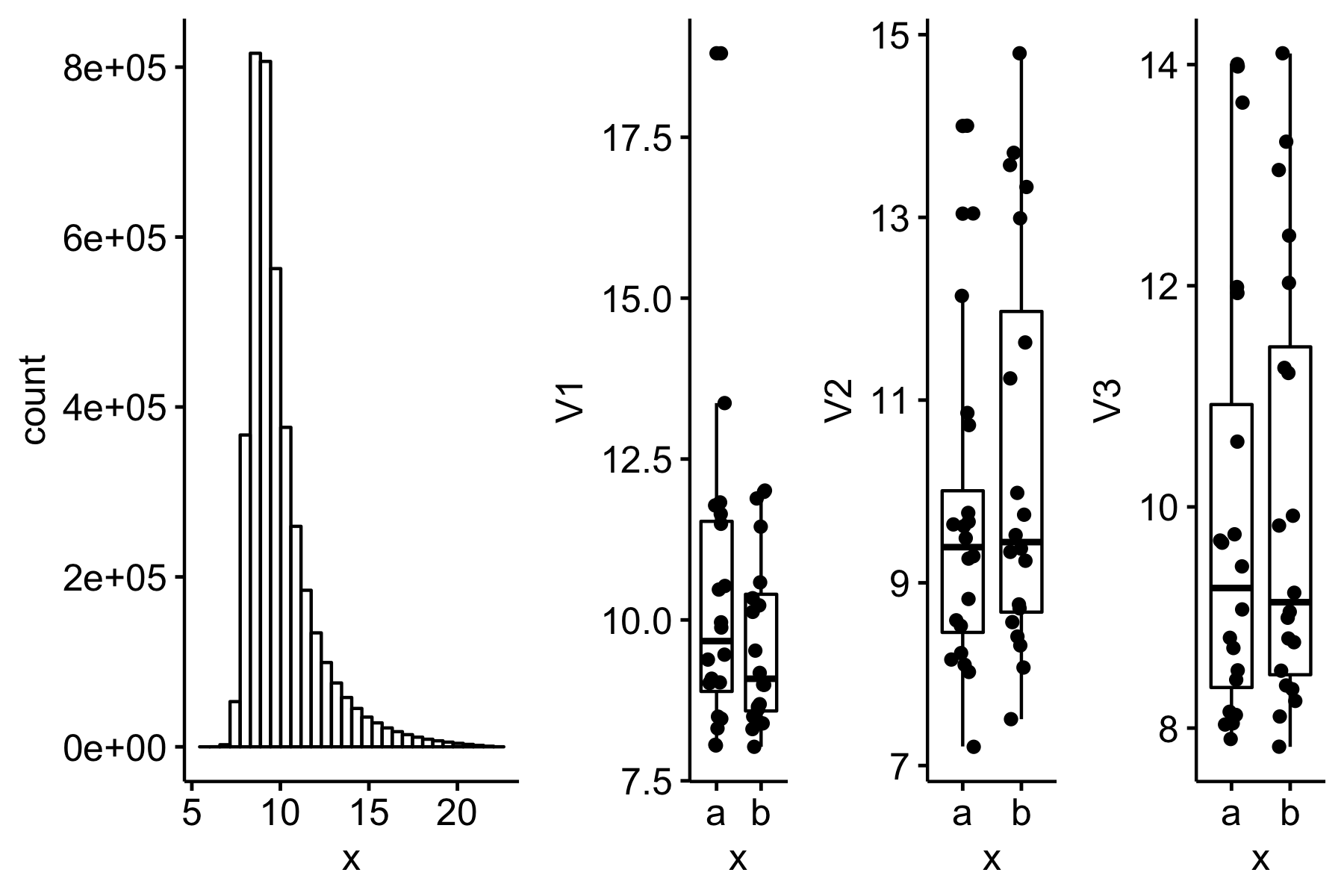
sigma = 0.8 (less approximately normal)

Figure 1: sigma = 0.8 (less approximately normal) 

knitr::include_graphics("2019-08-08-what-is-the-consequence-of-a-shapiro-wilk-test-of-normality-filter-on-type-i-error-and-power_files/figure-html/2019-08-08-gg-s=0.4.png")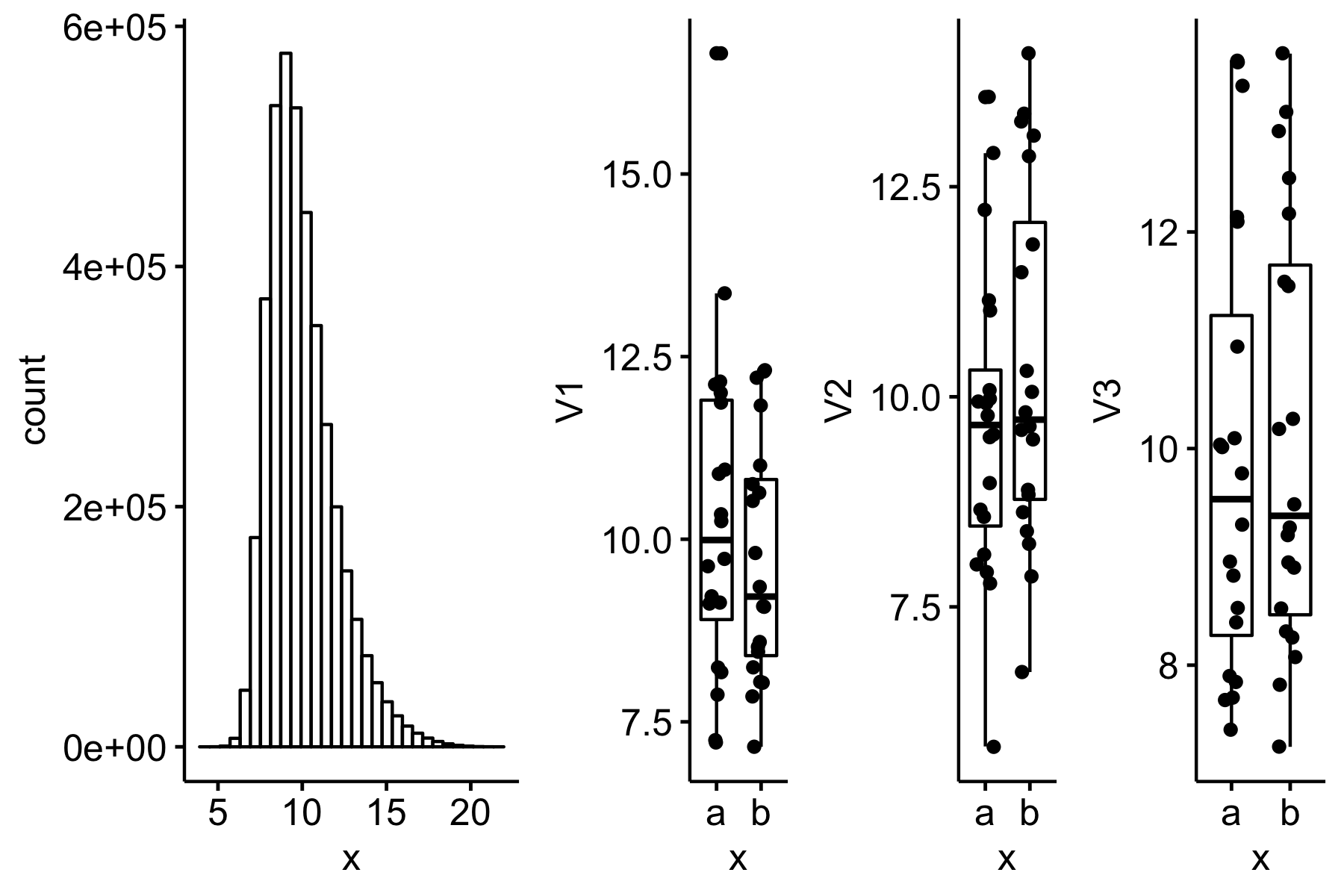
sigma = 0.4 (more approximately normal)

Figure 2: sigma = 0.4 (more approximately normal)

Type I error

type1 <- lognorm_table[, 1:6]
colnames(type1) <- c("n=6, sigma=.8", "n=10, sigma=.8", "n=20, sigma=.8", "n=6, sigma=.4", "n=10, sigma=.4", "n=20, sigma=.4")
row.names(type1) <- c(
  "iterations",
  "mu",
  "sigma",
  "effect",
  "Cn mean",
  "Cn sd",
  "Cn cv",
  "Tr mean",
  "Tr sd",
  "Tr cv",
  "n",
  "alpha for normality test",
  "failed normality, rate",
  "t-test: type I, unconditional",
  "t-test: type I, | pass",
  "t-test: type I, | fail",
  "MWW-test: type I, unconditional",
  "MWW-test: type I, | fail",
  "t-MWW: type I",
  "log t-test: type I, unconditional",
  "log t-test: type I, | fail",
  "t-log t: type I"
)
knitr::kable(type1, digits=3, caption="Type I error as a function of n and sigma for lognormal data")
Table 3: Type I error as a function of n and sigma for lognormal data
n=6, sigma=.8 n=10, sigma=.8 n=20, sigma=.8 n=6, sigma=.4 n=10, sigma=.4 n=20, sigma=.4
iterations 10000.000 50000.000 100000.000 10000.000 50000.000 100000.000
mu 0.000 0.000 0.000 0.000 0.000 0.000
sigma 0.800 0.800 0.800 0.400 0.400 0.400
effect 0.000 0.000 0.000 0.000 0.000 0.000
Cn mean 9.992 9.995 10.001 9.998 9.994 10.001
Cn sd 1.912 1.948 1.976 1.912 1.949 1.976
Cn cv 0.191 0.195 0.198 0.191 0.195 0.198
Tr mean 10.008 10.005 9.999 10.002 10.006 9.999
Tr sd 1.917 1.951 1.973 1.918 1.950 1.974
Tr cv 0.192 0.195 0.197 0.192 0.195 0.197
n 6.000 10.000 20.000 6.000 10.000 20.000
alpha for normality test 0.050 0.050 0.050 0.050 0.050 0.050
failed normality, rate 0.413 0.742 0.982 0.155 0.318 0.653
t-test: type I, unconditional 0.035 0.038 0.044 0.045 0.046 0.049
t-test: type I, | pass 0.054 0.093 0.230 0.049 0.057 0.072
t-test: type I, | fail 0.008 0.019 0.040 0.022 0.025 0.036
MWW-test: type I, unconditional 0.040 0.042 0.049 0.041 0.042 0.049
MWW-test: type I, | fail 0.029 0.035 0.047 0.042 0.041 0.044
t-MWW: type I 0.044 0.050 0.050 0.048 0.052 0.054
log t-test: type I, unconditional 0.039 0.043 0.047 0.048 0.048 0.049
log t-test: type I, | fail 0.014 0.025 0.044 0.030 0.032 0.040
t-log t: type I 0.038 0.043 0.048 0.046 0.049 0.051

Summary:

  1. All unconditional tests are slightly conservative (the Mann-Whitney-Wilcoxon least so)
  2. The conditional Type I error of the t-test for the sets that pass the Shapiro-Wilk filter increases with \(n\) but the rate of this increase is less for the parameterization generating data that is more approximately normal (mu = 0, sigma = 0.4)
  3. The overal Type I error for the normality-test filter strategy using the Mann-Whitney-Wilcoxon as the alternative is effectively the nominal value (0.05), or maybe a bit conservative at small \(n\) (0.044), regardless of the lognormal parameterization (over the small set explored)
  4. The overal Type I error for the normality-test filter strategy using the log transformed response as the alternative is effectively the nominal value (0.05), or maybe a bit conservative at small \(n\) (0.038), regardless of the lognormal parameterization (over the small set explored)

Power

type2 <- lognorm_table[, 7:12] # really power, not type 2
colnames(type2) <- c("n=6, sigma=.8", "n=10, sigma=.8", "n=20, sigma=.8", "n=6, sigma=.4", "n=10, sigma=.4", "n=20, sigma=.4")
row.names(type2) <- c(
  "iterations",
  "mu",
  "sigma",
  "effect",
  "Cn mean",
  "Cn sd",
  "Cn cv",
  "Tr mean",
  "Tr sd",
  "Tr cv",
  "n",
  "alpha for normality test",
  "failed normality, rate",
  "t-test: power, unconditional",
  "t-test: power, | pass",
  "t-test: power, | fail",
  "MWW-test: power, unconditional",
  "MWW-test: power, | fail",
  "t-MWW: power",
  "log t-test: power, unconditional",
  "log t-test: power, | fail",
  "t-log t: power"
)
knitr::kable(type2, digits=3, caption="Power as a function of n and sigma for lognormal response")
Table 4: Power as a function of n and sigma for lognormal response
n=6, sigma=.8 n=10, sigma=.8 n=20, sigma=.8 n=6, sigma=.4 n=10, sigma=.4 n=20, sigma=.4
iterations 10000.000 50000.000 100000.000 10000.000 50000.000 100000.000
mu 0.000 0.000 0.000 0.000 0.000 0.000
sigma 0.800 0.800 0.800 0.400 0.400 0.400
effect 1.600 1.600 1.600 1.600 1.600 1.600
Cn mean 9.997 9.995 10.001 9.998 9.994 10.001
Cn sd 1.913 1.948 1.976 1.912 1.949 1.976
Cn cv 0.191 0.195 0.198 0.191 0.195 0.198
Tr mean 11.603 11.605 11.599 11.602 11.606 11.599
Tr sd 2.224 2.263 2.289 2.224 2.262 2.290
Tr cv 0.192 0.195 0.197 0.192 0.195 0.197
n 6.000 10.000 20.000 6.000 10.000 20.000
alpha for normality test 0.050 0.050 0.050 0.050 0.050 0.050
failed normality, rate 0.398 0.739 0.980 0.157 0.317 0.647
t-test: power, unconditional 0.180 0.326 0.610 0.180 0.321 0.612
t-test: power, | pass 0.219 0.400 0.689 0.189 0.333 0.614
t-test: power, | fail 0.121 0.301 0.608 0.137 0.295 0.611
MWW-test: power, unconditional 0.245 0.491 0.849 0.175 0.332 0.661
MWW-test: power, | fail 0.288 0.533 0.852 0.225 0.415 0.703
t-MWW: power 0.246 0.498 0.849 0.194 0.359 0.672
log t-test: power, unconditional 0.225 0.392 0.728 0.199 0.350 0.660
log t-test: power, | fail 0.202 0.384 0.728 0.196 0.365 0.678
t-log t: power 0.212 0.388 0.728 0.190 0.343 0.656

Summary:

  1. The unconditional t-test of log transfored response and especially Mann-Whitney-Wilcoxon have more power than the unconditional t-test.
  2. The overal power of the normality-test filter strategy using the Mann-Whitney-Wilcoxon as the alternative is about the same as the unconditional MWW strategy with the more skewed parameterization but slightly higher than that for the unconditional MWW strategy with the less skewed parameterization.
  3. The overal power of the normality-test filter strategy using the log transformation as the alternative is about the same as the unconditional log transformation strategy regardless of the parameterization of the lognormal (over the space of my parameterization)

  1. Lumley, T., Diehr, P., Emerson, S., & Chen, L. (2002). The Importance of the Normality Assumption in Large Public Health Data Sets. Annual Review of Public Health, 23(1), 151–169. https://doi.org/10.1146/annurev.publhealth.23.100901.140546↩

  2. Rochon, J., Gondan, M., & Kieser, M. (2012). To test or not to test: Preliminary assessment of normality when comparing two independent samples. BMC Medical Research Methodology, 12(1). https://doi.org/10.1186/1471-2288-12-81↩